1) Miracles are of necessity very rare and improbable.
2) It is much more probable that the historical testimony is false than that the miracle actually occurred.
3) Therefore a wise man will not believe the historical testimony to the miracle since no testimony is sufficient to establish a miracle.
Hume's ultimate target is the New Testament miracles, especially Jesus' resurrection. However, he does not attack them directly, but uses indirect arguments. Hume is not saying that miracles are impossible and do not happen. What he is saying is that the evidence will always be insufficient to warrant belief.
1 Bayes Theorem
It has been said that one of the problems with Hume is that he was born before Bayes' Theorem. He wrote at a time when the mathematics of probability was in its infancy. Thus his argument is qualitative rather than quantitative. By a strange coincidence, Bayes' Theorem was proposed by Thomas Bayes (1702-1761), who was a British mathematician and a Presbyterian minister. Bayes' Theorem can be stated as P(A/B) = P(B/A) * P(A) / P(B), where P(A/B) means the probability that A will occur given that event B has already occurred. Bayes' Theorem is most easily understood by an example. I have taken this example from Wikipedia, but altered it slightly to reflect modern trends.
Suppose there is a school with 60 boys and 40 girls. 50% of girls wear trousers and 50% wear skirts. 5/6 of the boys wear trousers and (you guessed it) 1/6 boys wear skirts. If a student (of unknown gender) is wearing trousers, what is the probability that it is a girl?
Let A be, "The student is a girl" and B be, "The student is wearing trousers".
P(B/A) is that probability that a student is wearing trousers given that the student is a girl, which is 0.5 or 50%.
P(A) is the probability that a student is a girl, which is 0.4 or 40%.
P(B) is the probability that a student is wearing trousers. This is the probability that:
a) A student is a boy (0.6) * the probability that a boy is wearing trousers (5/6) +
b) A probability that a student is a girl (0.4) * the probability that a girl is wearing trousers (0.5).
Thus P(B) is the probability that a student is wearing trousers = 0.6 * 5/6 + 0.4 * 0.5 = 0.7.
Thus according to Bayes' Theorem P(A/B) = 0.5 * 0.4/0.7 = 2/7. i.e., the probability that a student is a girl given that the student is wearing trousers is 2 in 7.
This can be verified by the following table:
There are 60 boys and 5/6 wear trousers; therefore 50 boys wear trousers. There are 40 girls and 50% wear trousers; hence 20 girls wear trousers. Therefore, 20 out of 70 students who wear trousers are girls. Therefore P(A/B) = 2/7 as derived by Bayes' Theorem. So, behold it works.
Trousers
Skirts
Total
Boys
50
10
60
Girls
20
20
40
Total
70
30
100
Now I will apply Bayes' Theorem to miracles.
2 Application of Bayes' Theorem to Miracles
Let M be the event that a miracle occurred. Let R be the event that a report has been received that a miracle occurred. Then P(M/R) is the probability that a miracle occurred given that a report is received. According to Bayes' Theorem P(M/R) = P(R/M) * P(M) / P(R).
People tell the truth most of the time but occasionally what they say is wrong, either deliberately or unintentionally. Let us be uncharitable and denote an incorrect report by the event L (for Lie), and let T be a true report. Therefore, P(T) = 1 – P(L).
P(R/M) is the probability that a miracle is reported given that a miracle actually occurred. This is simply P(T), ie the witness reported truthfully.
P(M) is the probability that the miracle occurred in the first place.
P(R) is a bit trickier. This is the probability that a report of a miracle was received, whether true or false. Let M' (not M) be the event that the miracle did not occur. Then P(R) = P(M)*P(T) + P(M')*P(L).
For the purpose of this example, I will adopt Hume's assumptions on probabilities, although I will argue against them later. Hume argues that a miracle, by nature of the case, is highly improbable just based on the relative frequency of occurrence. Thus P(M) is a very small positive number. Hume would argue that there is at most one person who has risen from the dead (the rest being resuscitations). Thus, as far as the resurrection is concerned, P(M) is approximately 10-10 (based approximately on the total number of people who have existed during recorded history). Hume allows that people tell the truth much more often than not. So let us be generous (like Hume) and suppose that people lie less than 1% of the time. Then the application of Bayes' Theorem yields
P(M/R) = 9.9*10-9, which is a very small number.
So Hume seems to be right. If a single witness reported that a random person was raised from the dead, then it is highly improbable that the event actually occurred. This is Hume's core argument that the improbability of a miracle outweighs the reliability of human testimony.
However, what if multiple (n) independent witnesses reported the same event? The probability that they were all lying is P(L)n, which I will denote as Pn(L), which becomes vanishingly small as n increases. Conversely, Pn(T) asymptotes to 1 as n increases.
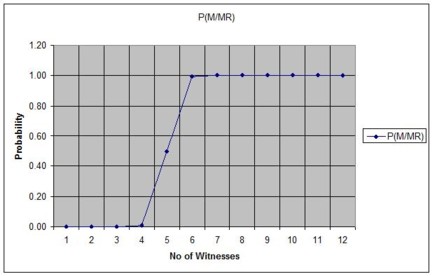
The following graph shows a plot of the probability that the miracle actually occurred against the number of independent witnesses (for the assumed values of P(M) and P(L)).
For this example, a wise man would believe that the miracle occurred if there were more than 5 independent witnesses.
You can argue all you like about appropriate values for P(M) and P(L). However, provided P(M) is non-zero there is always a value for the number of witnesses above which it would be wise to believe the report.
The above example is simplistic. Many factors contribute to an actual historical argument and these factors may be independent or interdependent. In most historical arguments it is difficult to assign agreed probabilities to each factor and derive a reliable result. Thus most historical arguments end up being qualitative rather than quantitative. However, the example demonstrates that multiple attestations may be sufficient to warrant belief in an improbable event. Thus Hume's core argument fails.
What I am saying is only common sense. It is something that is happening in our courts every day. There is a low probability that a random individual has committed a crime, but the weight of evidence may still be sufficient to secure a conviction beyond reasonable doubt.
3 The Probability of Miracles
In chapter 90 Hume states, "A miracle is a violation of the laws of nature; and as a firm and unalterable experience has established these laws, the proof against a miracle, from the very nature of the fact, is as entire as any argument from experience can possibly be imagined." From this Hume seems to be implying:
1) A miracle is a violation of the laws of nature.
2) The laws of nature are derived from our uniform experience and are a description of what always happens.
3) Thus by definition miracles never happen.
However something smells about this argument. It simply illustrates that the term "miracle" can be defined in such a manner as to be logically incoherent, such as a "married bachelor". On the contrary, the above argument could be modified as follows:
1) A miracle is a violation of the laws of nature.
2) The laws of nature are a description of what usually happens.
3) Thus a miracle is an unusual event.
Hume also seems to assign probabilities just based on relative frequencies. However, this approach is simplistic. For example, more people die from playing lawn bowls than from hang-gliding. Does that make lawn bowls a more dangerous sport? The context (e.g., age of participants) will affect the probability. In the same manner, the probability of Jesus' resurrection should not be based just on relative frequencies. It will be affected by background issues/beliefs, such as whether God exists and if He is interested in us. In this case, a person may well believe that P(M) is much greater than 10-10.
4 Witness Reliability
Hume's second argument is that no miracle has been attested by a sufficient number of reliable witnesses. In paragraph 92 Hume states,
"For first, there is not to be found, in all history, any miracle attested by a sufficient number of men, of such unquestioned good-sense, education, and learning, as to secure us against all delusion in themselves; of such undoubted integrity, as to place them beyond all suspicion of any design to deceive others; of such credit and reputation in the eyes of mankind, as to have a great deal to lose in case of their being detected in any falsehood; and at the same time, attesting facts performed in such a public manner and in so celebrated a part of the world, as to render the detection unavoidable: All which circumstances are requisite to give us a full assurance in the testimony of men."
A couple of comments can be made on this argument.
1) Firstly, he sets the bar very high. I doubt whether Hume would qualify himself. If we required the same witness credibility in court then the court system would get nowhere.
2) Secondly, he does not consider examples. What about the apostle Paul and Luke? I haven't got space to go into detail, but I think they come close.
5 Conflicting Miracle Claims
In his final section Hume claims that there are competing and conflicting historical miracle claims that essentially defeat one another. He cites a number of examples. I have not space to consider them all, but I will only discuss the example of the Roman emperor Vespasian. Hume states in section 96,
"One of the best attested miracles in all profane history, is that which Tacitus reports of Vespasian, who cured a blind man in Alexandria, by means of his spittle, and a lame man by the mere touch of his foot; in obedience to a vision of the god Serapis, who had enjoined them to have recourse to the Emperor, for these miraculous cures."
There are 2 issues with this example:
a) How strong is the historical attestation for Vespasian's miracles?
b) Would this miracle be in conflict with Biblical miracles?
Vespasian (9AD to 79AD) led the Roman army in subjugating the Jewish rebellion in 66AD. He became emperor in 69AD. While in Alexandria in Egypt in 69 AD Vespasian is purported to have healed a blind man and a lame man. These miraculous events were reported by the Roman historians:
a) Tacitus (56AD to 117AD) in Book 4 of his Histories (written about 100AD to 110AD),
b) Suetonius (69AD to 130AD) in Book 8 of the Lives of the Caesars (written about 119AD), and
c) Dio Cassius (about 155AD to 229AD) in book 65 of his Roman History (written after 200AD).
You can access these accounts at:
http://en.wikisource.org/wiki/The_Histories_(Tacitus)/Book_4
http://penelope.uchicago.edu/Thayer/E/Roman/Texts/Suetonius/12Caesars/Vespasian*.html
http://penelope.uchicago.edu/Thayer/E/Roman/Texts/Cassius_Dio/home.html
Hence we have 3 records by credible historians. Tacitus even records, "Persons actually present attest both facts, even now when nothing is to be gained by falsehood." Most historians agree that something unusual happened. However, there are causes for doubt. Tacitus elsewhere records that he did not believe it was a miracle and that he believed that the healings occurred by natural means. Dio Cassius records that the Alexandrians were unimpressed.
The Roman emperors were purported to be divine figures and any miraculous associations assisted an aspirant in obtaining power. Modern historians surmise that it was a setup by Vespasian's followers to enhance his aspirations for power. If we consider P(M) and P(L), we discover things are not so good. The Egyptian god Serapis has long since packed his bags and departed from public interest. So a coherent basis for the miracles is lacking. Thus P(M) is inordinately low. The historians were probably honest in their 2nd-hand reports of the stories but the promoters and witnesses at the time had a strong motivation for a positive account. Thus P(L) is high and the witnesses were probably not independent. So, do I believe it? Probably not.
The other issue is whether this is a conflicting miracle claim. In Matthew 24:24 Jesus is reported to say, "False Christs and false prophets will appear and perform great signs and miracles to deceive even the elect — if that were possible." This opens the possibility for miracles originating from "profane" sources.
Doubtless there have been many spurious claims regarding miracles. However, if 2 miraculous claims are inherently incompatible then at least one of them must lack sufficient evidence, but the fact that they conflict does not mean that both claims are false.
6 Conclusion
Hume states, "A wise man proportions his belief to the evidence." He goes on, however, to conclude that the consideration of historical evidence for a miracle is pointless, as a matter of principle.
I have not attempted to prove that miracles do occur. My purpose has been more modest. I have only attempted to show that a historical argument for the occurrence of a miracle can potentially be sufficient to warrant belief. My argument has shown that multiple attestations can in principle provide sufficient evidence to warrant belief in a miracle.
Kevin Rogers (Investigator 133) uses the inferential theorem of Reverend Thomas Bayes (1702 – 1761) to argue falsification of David Hume's claim that 'historical evidence' supporting miracles will always be insufficient to warrant belief in the miraculous. He accurately summarizes Hume's argument relating to 'frequency data', illustrates with an example using specified numbers of boys and girls, clad in trousers and/or skirts, and equates his example with a fundamentally different hypothetical investigation relating to undefined reported 'miracles' provided by an unspecified number of 'witnesses'. Using this assortment of 'eclectic methodology', he claims to demonstrate "multiple attestations may be sufficient to warrant belief in an improbably event".
Miracles and Probability
Bob Potter
(Investigator 134, 2010 September)
Note the important difference between his 'example', where 'the number' of subjects with 'two differences' (they wear trousers or skirts), are clearly specified whereas Kevin's 'hypothetical data' will relate to an 'open-ended' number of subjects (the world's population?) and an infinite possibility of 'differences' (miraculous happenings). Before identifying further flaws in Kevin's rationale, a few words defining and clarifying basic statistical terminology that might be helpful for readers unfamiliar with 'inferential statistics' and Bayes' theorem in particular.
A researcher should test an 'hypothesis' from a 'representative' sample from the target 'population' (being pedantic, this is never really possible; we can never be sure our sample is truly 'representative' — if we could, we wouldn't need a sample for testing, in the first place!). A 'hypothesis' normally takes the form that a given 'variable' will influence/cause subjects to behave in a particular way; an experiment will impose that variable on sample members, recording any resultant behavioural change. The obtained data will either support or not support the hypothesis.
Where
Bayes is different.
In most branches of science, statistical tests are used to 'test' beliefs and theories against reality, but this is not the case with Bayesian inference. Bayes requires not that beliefs (probabilities) and theories correspond to reality, rather that they are internally consistent (or 'cohere'). In contrast to the most commonly used procedures for 'testing probability', a Bayesian practitioner works not only with an hypothesis, but also with a specified predicted 'prior probability' that his test will evoke an expected probability outcome. As prominent Bayesian theoretician Lindley put it, "the theory…is only concerned with coherence; with how different views fit together, not with judgments of right and wrong. Perhaps the most obvious example of coherence is the way in which views prior to the data must cohere with those posterior to it: namely the Bayes' theorem."(1)
The whole slant of the Bayesian approach is that obtained evidence is not required to match the 'data' of the world 'out there', but to infer the probability that the opening (a priori) hypothesis might be true – 'truth' measured by its consistency with the hypothesis. Bayesian inference does not aspire to be objective, rather it relies upon (measurable) 'degrees of belief' — subjective probabilities. The most frequent criticism of the Bayesian approach arises from the status of the a posterior probability; after all, researchers may differ radically in their opinions regarding a population value. It is accepted from the outset, that an a posterior probability remains a statement of personal probability, that being the only kind of probability there is – the only way out of this dilemma for the Bayesian being that, in principle, the addition of more and more data, should cause the two positions to approach one another. Bearing the above in mind, we can now better understand some of Kevin's statistical flaws:
Witnesses
(subjects) must be 'independent'
This is a basic requirement of virtually every statistical test. Witnesses cannot be viewed as 'independent' if they are subject to influence from a fellow witness or group, especially if sharing critical or relevant beliefs: individual perceptions readily come together/transcend into group perceptions. Countless studies demonstrate the presence of others influences how an individual perceives an event; in addition, mistaken perception may be shared by all witnesses – how many members of the audience see the conjuror produce an egg from his ear? It is relatively easy to manipulate naïve Christian subjects into believing they are having a 'religious experience' when they are together at prayer. (2)
When it is reported that in Galilee, after Christ's crucifixion, Jesus was seen "by 500 brethren at one time", that may be independent witness evidence provided the person reporting the incident was himself present at the event. However, the only record comes from a Pauline letter. Paul was not there; he was reporting what he had been told. His evidence is 'hearsay'. A convert to the new religion (as a result of an experience on the road to Damascus — a 'religious experience'), he had to believe in the resurrection. (I am not suggesting Paul was dishonest or lying — I have no reason to doubt the sincerity of any biblical witness — such evidence is commonly reported in contemporary studies of conversion).
Assuming there were indeed 500 people present, not all could recognize or 'knew' Jesus (remember, a few days before, the Romans needed bribe Judas to identify Jesus!) — if it were a mass gathering of mostly 'true believers', the mass psychology of the occasion would engender a belief the person in question was indeed a 'resurrected being' — possibly not considered so unusual in those times!? There is no independent evidence of this event.
One of the most common errors in the application of Bayes Theorem is a failure by practitioners to take account of the lack of independence of the subjects/witnesses. This is especially true of groups of people sharing a strong belief/commitment shown a relevant 'happening'. Kevin recognizes the need for independence, but fails to consider that none of the Biblical resurrection 'witnesses' remotely approach 'independence' – indeed, the opening four verses of the gospel of Luke make it crystal clear that Luke himself purports to be doing no more than summarize (and edit) some of the contemporary hearsay reports in his possession.
Specify
the Miraculous details
It is acceptable for Kevin Rogers to select a statistical procedure allowing him to play with 'belief probabilities' rather than actual events; thus avoiding details of the 'miraculous event' – but he can't have it 'both ways' by arguing his example "demonstrates that multiple attestations may be sufficient to warrant belief in an improbable event". Remember, the Bayes' theorem focuses on 'belief probabilities', not events that actually happen. Kevin Rogers' findings do not demonstrate 'multiple attestations justify a belief' — rather that people might justifiably change their degree of belief, that 'prior opinions become less and less relevant to posterior opinion with additional data' — Bayesian inference argues a 'test' gives us 'test probabilities', not real probabilities!
From his graph, Kevin tells us any intelligent person would require only five independent witnesses to justify believing a miracle had occurred. But Kevin himself does not believe this nonsense! In discussion, almost a year ago, I referred Kevin to a Bill Bryson book where the author describes his decision to return to the States (from the UK) on learning that "3.7 million Americans, according to a Gallup Poll, believed that they had been abducted by aliens at one time or another"(3). In 1994, John E Mack, professor of Psychiatry at the Harvard Medical School published details of face-to-face interviews with more than eighty American citizens describing their 'alien abductions'. Thousands of hours of interviews convinced Mack these men, women and children were truthfully reporting authentic experiences…he describes, in great detail, their accounts of encounters with the 'beings' who transported their immobilized 'victims' to a spacecraft. (4) When it was pointed out to Kevin Rogers that Mack's book provides substantive evidence from a multitude of independent witnesses (compared with the inability of his Church to provide a single independent witness of Christ's resurrection!), it became clear Kevin was not prepared to discuss 'alien abductions'. Yet today he tells us, "a wise man would believe that the miracle occurred if there were more than five independent witnesses".
All Luke's gospel (including 'Acts') evidence is hearsay. Were there a document, signed by one of the two apostles who encountered Jesus on the road to Emmaus, we might accept it as 'independent' witness statement and acceptable as evidence…but one wonders what credence we might give these two 'witnesses'. Consider 'the facts'. Two members of Christ's 'inner circle', walked and discussed with Jesus for several hours (the same Jesus they had associated with up to a few days previously), yet failed to recognize him during their very inter-active longish walk to Emmaus. Are these the individuals we might take to a modern-day 'identification parade', looking for the guilty person? All Luke's 'hearsay' reportage of encounters between disciples and the 'risen Lord' echo this same problem. For several years previously, the disciples witnessed Jesus perform numerous 'miracles'; the raising of Lazarus, blind men given sight, devils cast out — yet when Jesus returns, in the same physical form, as he had previously assured them he would, albeit with wounded hands and feet, they have difficulty recognizing him. Even, as he ascends into the clouds (quite literally) two angels are waiting to re-assure 'the eleven' that it was indeed their late 'teacher' who ascended into the sky…and that he will return!
I read Tom Paine's The Age of Reason in my teenage years and was astounded at his identification of the conflicting accounts of the Resurrection in the four gospels. Christians replied to me it was common knowledge that if a dozen people witnessed a road accident and all twelve were obliged to write independent reports of what had taken place, the outcome would be twelve quite different accounts. At first I thought this to be a very reasonable reply. But the argument has its limits. If it was my Dad driving one of the cars, I can't imagine imagining it was the next-door neighbour. If an earthquake opened cracks in the road and dead bodies emerged from the nearby cemetery and inspected the debris in their shrouds, I can't imagine most present not hearing and feeling the earth move — hardly trivial happenings, but the events described by Matthew, find no corroboration elsewhere. With the absence of independent witnesses, I cannot see how Kevin can even begin with his statistics!
References:
(1) Lindley, D. V. Bayesian Statistics in Harper & Hooker (eds) Foundations of Probability Theory, Statistical Inference and Statistical Theories of Science: Reidel (1976) p 435.
(2) Pahnke, W. N. The Religious Experience in Psychedelic Review (1964) p324-346.
(3) Bryson, Bill Notes from a Small Island Black Swan (1995) p34.
(4) John E Mack Abduction: Human Encounters with Aliens Simon & Schuster (1994)
In Investigator #133 I presented a critique of "On Miracles" by the Scottish Enlightenment philosopher, David Hume (1711-1776). Hume's primary argument was that we should never believe a report of a miracle, as the likelihood of a false report would always outweigh the chance of the miracle actually occurring. I argued that multiple attestations to the same event from a sufficient number of independent witnesses could provide sufficient evidence to warrant belief. In Investigator #134 Bob Potter critiqued my argument.
Hume, Miracles and Probability
Kevin Rogers
(Investigator 136, 2010 January)
Baye's Theorem states, P(A/B)*P(B) = P(B/A)*P(A), where P(A/B) means the probability that A occurred given that B has already occurred. For example, what is the probability that it will rain, given that there are clouds in the sky? Baye's Theorem allows us to calculate conditional probabilities. There are 4 terms in the equation. If we know 3 of them then we can calculate the 4th. I demonstrated Baye's Theorem with an example concerning boys and girls wearing trousers and skirts at school. Bob claimed that I equated my tutorial example with the argument on miracles. This is not true. The purpose of the example was only to illustrate the use of Baye's Theorem. I then reapplied Bayes's Theorem to the argument regarding miracles.
Bob claims that my example contained a known number of students whereas miracles involve an unknown number of subjects. This is true, but Bayes Theorem is always true, whether the number of members in the set is defined or not. With large undefined samples the 3 "known" terms in general have to be estimated. The answer is only as accurate as the input data. Since my argument was an in-principle argument, the initial estimates of the input parameters are not relevant. This supposedly was my initial flaw and Bob claims further flaws.
Bob goes on to provide a discussion of "Bayesian Inference". Bob has confused Baye's Theorem with Bayesian Inference. Bayesian Inference is a form of qualitative argument that is based on Baye's Theorem, whereas Baye's Theorem is a simple quantitative mathematical formula. If you would like to see good examples of the use of Bayesian Inference, then read Richard Swinburne's books on "The existence of God" and "The Resurrection of God Incarnate".
Bob then proceeds to use a whole pile of big words, convoluted sentences, plenty of underlining and bolding. I think we are supposed to be impressed by his great learning. At the end he concludes, "We can now better understand some of Kevin's statistical flaws." Can we? Did you? Was it the bolding or underlining that did it? The conclusion appears like a rabbit out of a hat. The conclusion is unrelated to his argument.
Bob then goes on to claim that witnesses must be independent, as dependent witnesses can affect each other. I wholeheartedly agree, as this was what I stated in my original article. However, Hume's primary argument was an "in-principle" argument and I provided an in-principle objection. Neither Hume nor I were considering specific examples.
Fortunately Bob and I are actually in agreement. Bob doesn't believe David Hume either, for Bob then proceeds to raise historical arguments about the resurrection. If Bob actually believed David Hume, then he wouldn't have bothered. The essence of Hume's argument is that the issue of miracles is not worth discussing, but Bob then goes on to discuss the evidence. Bob, I am on your side. I agree with you that David Hume is wrong.
Bob goes on to argue that I do not believe my own argument because I do not believe in alien abductions despite the large number of witnesses.
My reasons for not believing in alien abductions are the initial implausibility and that there tend not to be independent witnesses to the same event. It seems implausible because of the huge distances involved. It would require a nuclear powered spaceship with nearly 100% efficiency to accelerate a spaceship near to the speed of light. Even then it would require a large number of years to travel from the nearest viable star. In addition I do not know of any cases where there are multiple independent witnesses to the same event. Instead, there are multiple witnesses to different events. I actually do believe Hume's argument where there is a single witness to a single event. Given the large population of earth there are bound to be odd individuals who will lie or be deluded and provide a strange report. However, their stories are not generally corroborated by multiple independent witnesses. There are numerous instances of multiple witnesses attesting to seeing a UFO. However, this does not necessarily mean that the UFO is an alien. I am actually agnostic on the subject. If I could be shown that there were multiple witnesses to the same event then I would have to reconsider my position. Apart from this, I haven't done much research on the issue.
Bob also mentions that multiple people may see a conjurer produce an egg from his ear. This is a bad argument. The multiple witnesses do not actually believe that the conjurer produced an egg from their ear. They know it is a trick. The multiple witnesses will uniformly testify that they were tricked; and they would be right.
My argument against David Hume is nothing new. Hume's argument has been debunked many times before and it is widely accepted within philosophical circles that Hume's argument is wrong. However, there is a false perception amongst sceptics that Hume has issued the final word. You don't have to understand Baye's Theorem to appreciate that Hume is wrong. If there are multiple independent witnesses to the same event then this provides stronger evidence that the event actually occurred. This is just common sense and is basic to police investigations and for court proceedings.
I agree with Bob that the apostolic witness to the resurrection is not a clear cut case of multiple independent witnesses. The actual situation is far more complicated and involves a mixture of independent and dependent testimony. However, I think we can dispense with David Hume's in-principle argument and look at the actual nature of the evidence, but that will have to be dealt with another time.